Symmetrical component analysis
Summary
1.소개
2.대칭 좌표법으로의 변환
3.Sequence network for PS component
4.Sequence network for power system
1. 소개
평형고장에서는 한상을 기준으로 분석할수가 있다.
왜냐하면 모든 상은 크기가 동일하고 위상은 120도 떨어져 있기때문에 한상의 전류와 전압을 안다면 다른상의 전류와 전압을 알수있다.
하지만 다른 타입의 고장(불평형고장)에는 일반적인 방법으로는 구해내기가 힘들기 때문에 대칭좌표법이라는 수학적인 테크닉을 사용하여 풀어낸다.
2. Symmetrical Component Transformation
-C.L.Fortescue 가개발
-3상시스템의 분석과 디자인을 위한 모델링 기법
-3상의 네트워크를 3상의 더간단한 네트워크로 연결
-불평형 회로에서 3개의 시퀀스 네트워크는 불평형일때만 연결된다.
-3상 시스템을 분석하는 강력한툴
-불평형 작동중의 복잡한 현상을 간단한 텀으로 나타낸다
-시퀀스 네트워크는 3상 네트워크의 결과를 얻기위해 겹쳐져야 한다.
단점을 굳이 꼽자면 이있다면 먼저 상의 대칭성분을 구하고나서
전류 전압값을 구하고 그걸다시 실제 값으로 변환해야한다.
제가 하는 것의 최종목표는 3상 시스템을 또다른 3상 시스템의 세트로 바꾸어서
불평형 고장을 계산하는 것 입니다. 그것은 조금있다가 활용해볼것이고
일단 지금은 3상의 요소를 9개의 요소로 바꾸는 것을 보여 드리겠습니다.
대충은 아시겠지만 일단 복습한다는 의미로 편안히 봐주시면 되겠습니다.

우선 첫번쨰는 정상순의 요소입니다. 3개의 대칭분으로 이루어지고
크기가 같으며 120도 씩 떨어져 있습니다.
저희가 눈여겨 봐야 할것은 실제 상의 순과 같다는 것입니다.

두번째는 역상순 요소들입니다. 마찬가지로 3개의 대칭분
크기가 같고 120도 씩 떨어져 있습니다
저희가 눈여겨 봐야할것은 실제 상의 순과 역방향을 이룹니다.

마지막은 영상분의 요소들입니다. 3개의 요소로 이루어져있으며 크기는 같고
상순 즉 순서의 개념이 없는 친구들입니다.

이것은 실제로 3상을 대칭분으로 나타냈을때의 그림입니다.
보시면 a상이 a상의 영상분 정상분 역상분 이렇게 나누어져있는걸 보실수 있고
나머지도 마찬가지인것을 볼수있습니다.
이게 그냥 보면 이해가 잘안갈수 있으니 좀 역동적으로 보여드리겠습니다.
http://Stevenblair.github.io/seq

이제는 이렇게 대칭성분을 이용하여 상하나를 나타내는 것을 수학적인 식으로
나타내보겠습니다.
자 먼저 아셔야 할것은 이제부터는 a상을 reference로 볼것이기 때문에
따로 옆에 이작은 글자에 적지 않을 것입니다.
자 이게 무슨소리냐면 원래라면
V(a)=V(a0)+V(a1)+V(a2)
V(b)=V(b0)+V(b1)+V(b2)
V(c)=V(c0)+V(c1)+V(c2)
이렇게 나타내지는 것이 맞습니다만. 이 그림을 보시면 그렇게 나타나있지가 않습니다.
이것이 어떻게 가능하냐면 바로 a상이 reference 기준축이 되는것과,
A오퍼레이터 라는것에 의하여 가능해 집니다.
우선 a오퍼레이터라는건 1의 크기를 가지며 120도의 위상각을 가지는 요소입니다.
이것이 어떻게 작용을 하냐면 V(b1)이나 V(b2) 를 a상의 대칭분으로 나타내는게 가능해집니다. 예를 들자면 여기 b상의 a^2*V(1)이라는건 V(a1)을 a^2을 곱하여 V(b1)을 나타냈다는 뜻입니다. 또한 b상의 a*V(2) 라는것은 사실 V(a2)를 a^2을 곱해서 V(b2)를
나타냈다는 뜻입니다. 즉 여기 적혀있는 요소들은 전부 a상을 기준으로 치환이 되어있며 작은 숫자 옆에 a가 전부 생략되어 있습니다.
그리고 이것을 행렬로 나타내면 이런식을 나타내게 되고 여기 이행렬을 A행렬이라고 합니다.

식을 더욱 간단하게 나타낸 결과입니다.
상의 요소를 대칭분으로 바꾸는것을 알았으니 반대로 대칭분을 상의 요소로 표현하는것을 알아보겠습니다. 간단합니다. 위 행렬식에서 A행렬을 역행렬을 취해주면 대칭분요소를 상의 요소로 나타내는 것이 가능합니다. A의 역행렬은 미리 계산을 해두었습니다.
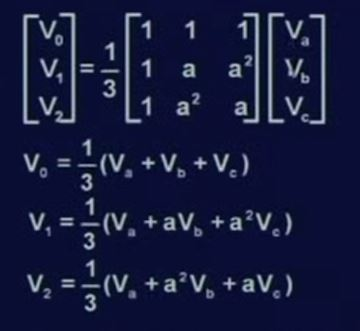
수학적인 계산을 통해서 이렇게 나온다는것을 알수있구요.
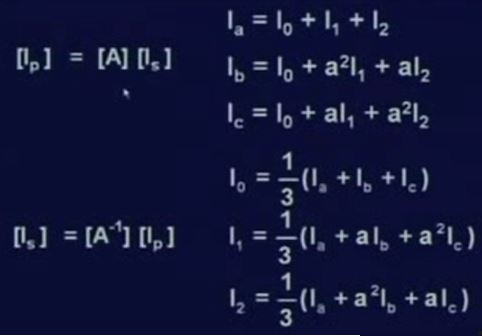
V가 이렇게 나올수가 있듯이 I도 마찬가지로 대칭분으로 똑같이 나타낼수있습니다.
자 여기까지해서 상의 요소와 대칭요소를 서로 변환하는것을 알게됬습니다.
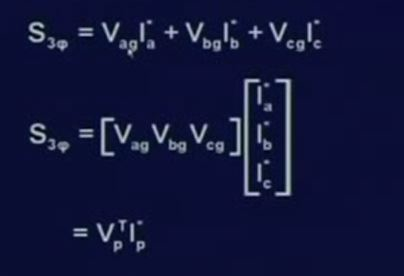
이것은 3상 파워 입니다. 3상 파워 를 구하려면 각상의 전압과 전류의 CONJUGATE한것을 더하면 된다는 것을 알고있습니다. 이것을 행렬로 나타내면 이렇게됩니다.
3상파워또한 대칭분으로 나타내 볼것입니다.

아까 만든식중에 상의 요쇼를 대칭분으로 나타낼수가 있습니다.
그렇게 하면 이렇게 나타내지고 행렬의 규칙으로 인해서 전치행렬은 앞뒤가 바뀌고
위와 같이 계산됩니다.

A전치행렬과 A의 복수 복소행렬을 곱하면 이렇게 대칭요소만 남는 형태가 되구요

그렇게되면 3상 파워는 대칭분으로 나타낼수도 있습니다.
여기서 중요한것은 대칭좌표에서도 파워에 대한식은
일반상으로 계산한 파워식과 같다는것입니다.
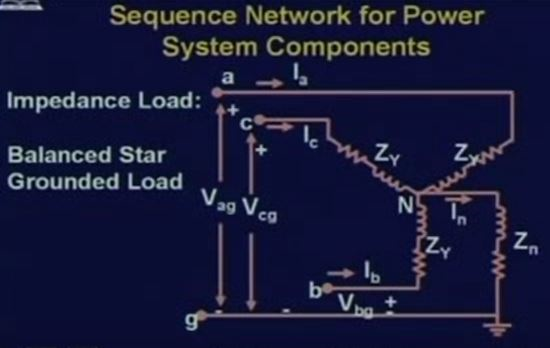
다음으로 할것은 3상Y결선의 LOAD를 대칭좌표법을 이용하여 표현해 보겠습니다.
여기서 주목해야 할것은 임피던스 행렬을 유심히 살펴봐야합니다.

수식으로 나타내면 위와같이되고 I(n)은 abc상의 합으로 나타낼수 있기때문에 치환할수 있습니다. 그러면 b상 c상도 마찬가지가 됩니다.

이것또한 행렬을 통하여 표현하면 위와 같이됩니다.
더욱 편하게 나타내면 vp=zpip가 됩니다. 여기서 아까 배운 대칭좌표법
의 식에서 vp와 ip를 대칭좌표로 치환해줍니다. 그리고 vs의 A를 역행렬을
취해주면 Zs로 나타낼수 있습니다. 이 임피던스 행렬을 계산해주면

이렇게 나오는데 여기서 저희가 주목해야 할 차이점은 임피던스 상행렬과 달리
임피던스행렬의 대칭성분은 대각 행렬이라는 점입니다. 이것이 어떤의미냐면
우선 상의 임피던스 행렬은 zn이라는걸로 서로 연결이 되어있습니다. 무슨말이냐면
상의 공식을 보면 a상의 전압을 구할때 zn을 통해서 ib와 ic가 관련이 되어있습니다.
마찬가지로 b상 c상도 마찬가지 입니다. 그리고 여기에서는 다루지 않았지만 실제로는 상호 임피던스라는 것도 있는데 그것을 통해서도 관련이 됩니다. 물론 여기서는 상호 임피던스가 0라고 가정하였습니다.
반대로 3개의 대칭성분 회로는 .상이 평형일때 독립적입니다. 서로 연결되지않는다 . 서로 관련되지않는다. 이런 뜻입니다. 이것은 상을 각 시퀀스 회로로 분석하는것을 허용하는 것이기 때문에 굉장히 중요한 개념입니다.
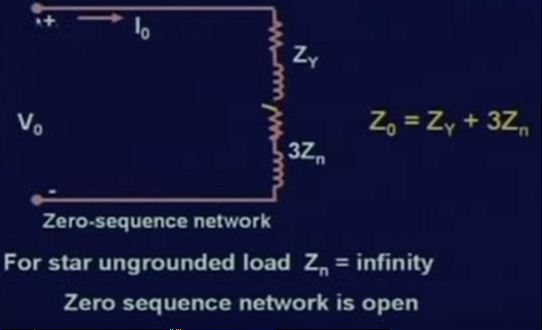
그래서 실제로 대칭성분들의 수식에 의거하여 회로를 만들어 본다면
영상분은 이렇게 됩니다. 지금 그림은 이렇게 open되어 있는데 이것이 무슨뜻이냐면
만약 처음보았던 부하 회로가 그라운딩이 된 회로라면 Zn은 존재하지만
그라운딩이 되지않은 회로라면 그회로는 Zn이 무한대가 되는것과 마찬가지이며
회로가 open 상태인것과 다름없습니다. 이것은 zero 시퀀스가 open이게되며
영상전류도 흐를수 없다는것을 뜻합니다.
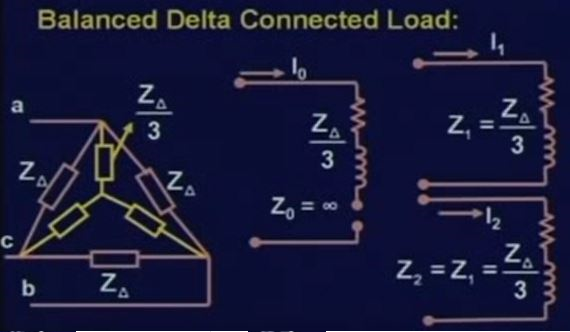
다음은 델타 회로를 이용하여 만들어 보겠습니다.
우선 델타성분들을 star결선등가회로로 바꾸어서 이때까지 배운 식에 의거하여
회로를 구성하여 줍니다. 그렇게하면 이렇게 독립적인 회로를 만들게 되고
아까 말했듯이 Zn이 없는경우 영상분의 회로는 open 된것이나 마찬가지가 됩니다.
그래서 delta회로는 영상분전류가 흐를수가 없습니다.

이젠 일반적인 상 임피던스에 대해서 대칭성분으로 변환해 보겠습니다.

아까 전에 배운 임피던스 행렬의 수식에 의하여 다음과 나타낼수 있는데
아까 와 다른것이 어떤거냐면 상임피던스가 아까는 구체적으로 나온것인
반면 지금의 상임피던스는 자기임피던스와 상호임피던스를 통하여 나타내고
있습니다.
이것을 수식으로 나타낼시 다음과 같습니다.

이렇게 복잡한 수식이 나오게 되는데요.

만약 부하가 대칭부하라면 다음과 같은 조건이 만족되게 됩니다.
우선 자기 임피던스는 다같게되고 상호임피던스 또한 같게 됩니다.
그렇게 되면 임피던스행렬의 비대칭 성분은 전부 0이되며 대칭성분만 위와 같이 남게 됩니다.
'전기기사' 카테고리의 다른 글
| 2021 전기기사 김상훈 커넥츠 강의표 (0) | 2021.01.03 |
|---|---|
| 불평형 고장 , Asymetrical Fault Analysis (0) | 2020.11.08 |
| PU법, 단위법 (0) | 2018.12.26 |
| 2013년06월02일 기출문제 (0) | 2018.12.18 |
| 2013년03월10일 기출문제 (0) | 2018.12.18 |


댓글